哈哈博客
所有文章 分类
哈哈博客

目录

Java基础算法

 收录于 java知识
   约 4069 字   预计阅读 9 分钟 

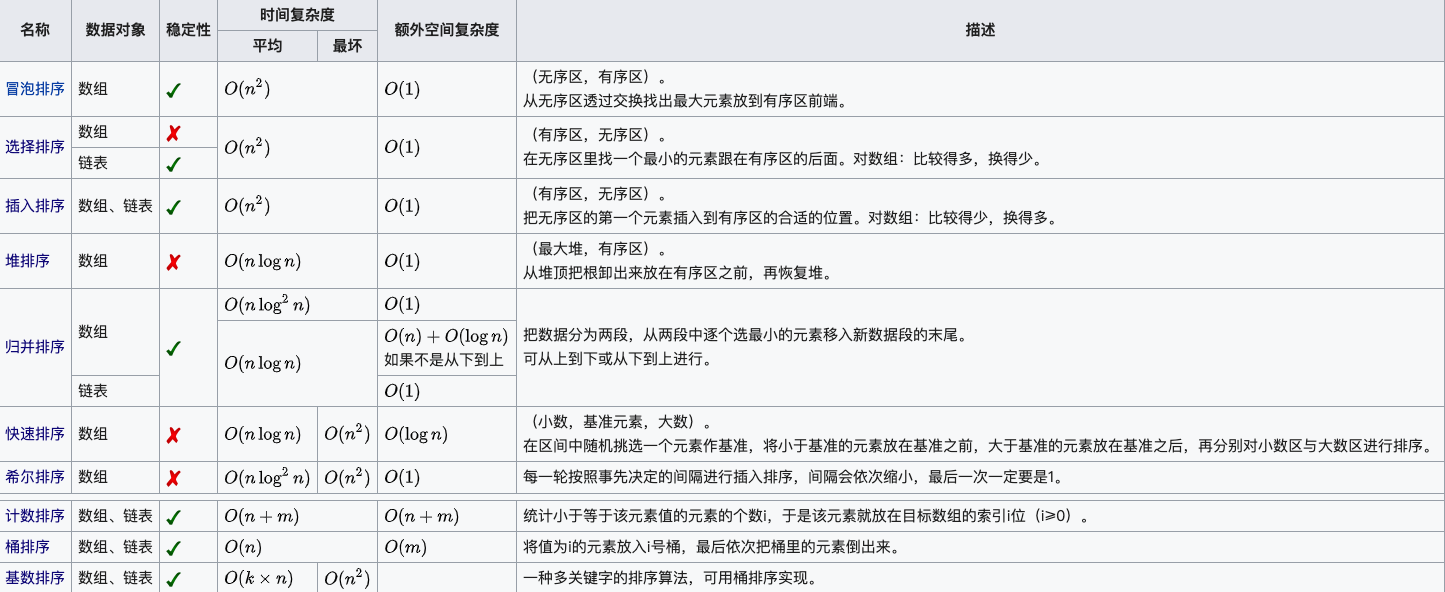
复杂度

/img/Java基础算法/1.png

冒泡排序

冒泡排序

基本原理：

  1. 对于给定的n个记录，从第一个记录开始依次对相邻的两个记录进行比较，
  2. 当前面的记录大于后面的记录时，交换位置，
  3. 进行一轮比较和换位后，n个记录中的最大记录将位于第n位；
  4. 然后对前(n-1)个记录进行第二轮比较；重复该过程直到进行比较的记录只剩下一个为止。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

/**
 * @className: BubbleSort
 * @description: 冒泡排序
 * @author: hahaen
 **/
public class BubbleSort {
    public static void main(String[] args) {
        int[] arr = {1, 1, 2, 0, 9, 3, 12, 7, 8, 3, 4, 65, 22};

        BubbleSort.bubbleSort(arr);

        for (int i : arr) {
            System.out.print(i + ",");
        }
    }

    private static void bubbleSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            // 设定一个标记，若为true，则表示此次循环没有进行交换，也就是待排序列已经有序，排序已经完成。
            boolean flag = true;

            for (int j = 0; j < arr.length - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    int tmp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = tmp;

                    flag = false;
                }
            }

            if (flag) {
                break;
            }
        }
    }
}

选择排序

选择排序

基本原理：

  1. 对于给定的一组记录，经过第一轮比较后得到最小的记录，
  2. 然后将该记录与第一个记录的位置进行交换；
  3. 接着对不包括第一个记录以外的其他记录进行第二次比较，
  4. 得到最小的记录并与第二个记录进行位置交换；
  5. 重复该过程，直到进行比较的记录只有一个为止。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

/**
 * @className: SelectSort
 * @description: 选择排序
 * @author: hahaen
 **/
public class SelectSort {
    public static void main(String[] args) {
        int[] arr = {1, 1, 2, 0, 9, 3, 12, 7, 8, 3, 4, 65, 22};

        SelectSort.selectSort(arr);

        for (int i : arr) {
            System.out.print(i + ",");
        }
    }

    public static void selectSort(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            int min = i;

            // 每轮需要比较的次数 N-i
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] < arr[min]) {
                    // 记录目前能找到的最小值元素的下标
                    min = j;
                }
            }

            // 将找到的最小值和i位置所在的值进行交换
            if (i != min) {
                int tmp = arr[i];
                arr[i] = arr[min];
                arr[min] = tmp;
            }

        }
    }
}

插入排序

插入排序

基本原理：

  1. 对于给定的一组数据，初始时假设第一个记录自成一个有序序列，
  2. 其余记录为无序序列。接着从第二个记录开始，按照记录的大小依次将当前处理的记录插入到其之前的有序序列中，
  3. 直至最后一个记录插入到有序序列中为止。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

/**
 * @className: InsertSort
 * @description: 插入排序
 * @author: hahaen
 **/
public class InsertSort {
    public static void main(String[] args) {
        int[] arr = {1, 1, 2, 0, 9, 3, 12, 7, 8, 3, 4, 65, 22};

        InsertSort.insertSort(arr);

        for (int i : arr) {
            System.out.print(i + ",");
        }
    }

    private static void insertSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {

            // 记录要插入的数据
            int tmp = arr[i];

            // 从已经排序的序列最右边的开始比较，找到比其小的数
            int j = i;
            while (j > 0 && tmp < arr[j - 1]) {
                arr[j] = arr[j - 1];
                j--;
            }

            // 存在比其小的数，插入
            if (j != i) {
                arr[j] = tmp;
            }

        }
    }
}

希尔排序

希尔排序

基本原理：

  1. 先将待排序的数组元素分成多个子序列，使得每个子序列的元素个数相对减少，
  2. 然后对各个子序列分别进行直接插入排序，待整个待排序序列"基本有序后"，
  3. 最后再对所有元素进行一次直接插入排序。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

/**
 * @className: ShellSort
 * @description: 希尔排序
 * @author: hahaen
 **/
public class ShellSort {
    public static void main(String[] args) {
        int[] arr = {1, 1, 2, 0, 9, 3, 12, 7, 8, 3, 4, 65, 22};

        ShellSort.shellSort(arr);

        for (int i : arr) {
            System.out.print(i + ",");
        }
    }

    private static void shellSort(int[] arr) {
        int length = arr.length;
        int temp;
        for (int step = length / 2; step >= 1; step /= 2) {
            for (int i = step; i < length; i++) {
                temp = arr[i];
                int j = i - step;
                while (j >= 0 && arr[j] > temp) {
                    arr[j + step] = arr[j];
                    j -= step;
                }
                arr[j + step] = temp;
            }
        }
    }
}

归并排序

归并排序

基本原理：

  1. 利用递归与分治技术将数据序列划分成为越来越小的半子表，
  2. 再对半子表排序，最后再用递归方法将排好序的半子表合并成为越来越大的有序序列。
  3. 对于给定的一组记录(假设共有n个记录)，
  4. 首先将每两个相邻的长度为1的子序列进行归并，
  5. 得到n/2(向上取整)个长度为2或1的有序子序列，
  6. 再将其两两归并，反复执行此过程，直到得到一个有序序列。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

import java.util.Arrays;

/**
 * @className: MergeSort
 * @description: 归并排序
 * @author: hahaen
 **/
public class MergeSort {
    public static void main(String[] args) {
        int[] arr = {1, 1, 2, 0, 9, 3, 12, 7, 8, 3, 4, 65, 22};
        mergeSort(arr);
        System.out.println(Arrays.toString(arr));
    }

    public static void mergeSort(int[] arr) {
        //在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
        int[] temp = new int[arr.length];
        sort(arr, 0, arr.length - 1, temp);
    }

    private static void sort(int[] arr, int left, int right, int[] temp) {
        if (left < right) {
            //左边归并排序，使得左子序列有序
            int mid = (left + right) / 2;
            sort(arr, left, mid, temp);
            //右边归并排序，使得右子序列有序
            sort(arr, mid + 1, right, temp);
            //将两个有序子数组合并操作
            merge(arr, left, mid, right, temp);
        }
    }

    private static void merge(int[] arr, int left, int mid, int right, int[] temp) {
        //左序列指针
        int i = left;
        //右序列指针
        int j = mid + 1;
        //临时数组指针
        int t = 0;
        while (i <= mid && j <= right) {
            if (arr[i] <= arr[j]) {
                temp[t++] = arr[i++];
            } else {
                temp[t++] = arr[j++];
            }
        }
        //将左边剩余元素填充进temp中
        while (i <= mid) {
            temp[t++] = arr[i++];
        }
        //将右序列剩余元素填充进temp中
        while (j <= right) {
            temp[t++] = arr[j++];
        }
        t = 0;
        //将temp中的元素全部拷贝到原数组中
        while (left <= right) {
            arr[left++] = temp[t++];
        }
    }
}

快速排序

快速排序

基本原理：

  1. 对于一组给定的记录，通过一趟排序后，将原序列分为两部分，
  2. 其中前一部分的所有记录均比后一部分的所有记录小，
  3. 然后再依次对前后两部分的记录进行快速排序，
  4. 递归该过程，直到序列中的所有记录均有序为止。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

/**
 * @className: QuickSort
 * @description: 快速排序
 * @author: hahaen
 **/
public class QuickSort {
    public static void main(String[] args) {
        int[] arr = {1, 1, 2, 0, 9, 3, 12, 7, 8, 3, 4, 65, 22};

        QuickSort.quickSort(arr, 0, arr.length - 1);

        for (int i : arr) {
            System.out.print(i + ",");
        }
    }

    private static void quickSort(int[] arr, int left, int right) {

        if (left < right) {
            int partitionIndex = partition(arr, left, right);
            quickSort(arr, left, partitionIndex - 1);
            quickSort(arr, partitionIndex + 1, right);
        }
    }

    private static int partition(int[] arr, int left, int right) {
        // 设定基准值（pivot）
        int pivot = left;
        int index = pivot + 1;
        for (int i = index; i <= right; i++) {
            if (arr[i] < arr[pivot]) {
                swap(arr, i, index);
                index++;
            }
        }
        swap(arr, pivot, index - 1);
        return index - 1;
    }

    private static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

堆排序

堆排序

基本原理：

  1. 对于给定的n个记录，初始时把这些记录看作一颗顺序存储的二叉树，
  2. 然后将其调整为一个小顶堆，然后将堆的最后一个元素与堆顶元素进行交换后，
  3. 堆的最后一个元素即为最小记录；接着讲前(n-1)个元素重新调整为一个小顶堆，
  4. 再将堆顶元素与当前堆的最后一个元素进行交换后得到次小的记录，
  5. 重复该过程直到调整的堆中只剩一个元素时为止，该元素即为最大记录，
  6. 此时可得到一个有序序列。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

/**
 * @className: HeapSort
 * @description: 堆排序
 * @author: hahaen
 **/
public class HeapSort {
    public static void main(String[] args) {
        int[] arr = {1, 1, 2, 0, 9, 3, 12, 7, 8, 3, 4, 65, 22};

        HeapSort.heapSort(arr, arr.length);

        for (int i : arr) {
            System.out.print(i + ",");
        }
    }

    private static void heapSort(int[] arr, int len) {

        buildMaxHeap(arr, len);

        for (int i = len - 1; i > 0; i--) {
            swap(arr, 0, i);
            len--;
            heapify(arr, 0, len);
        }
    }

    private static void buildMaxHeap(int[] arr, int len) {
        for (int i = (int) Math.floor(len / 2); i >= 0; i--) {
            heapify(arr, i, len);
        }
    }


    private static void heapify(int[] arr, int i, int len) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int largest = i;

        if (left < len && arr[left] > arr[largest]) {
            largest = left;
        }

        if (right < len && arr[right] > arr[largest]) {
            largest = right;
        }

        if (largest != i) {
            swap(arr, i, largest);
            heapify(arr, largest, len);
        }
    }

    private static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

计数排序

计数排序

基本原理：

  1. 找出待排序的数组中最大和最小的元素
  2. 统计数组中每个值为i的元素出现的次数，存入数组C的第i项
  3. 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）
  4. 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

/**
 * @className: CountingSort
 * @description: 计数排序
 * @author: hahaen
 **/
public class CountingSort {
    public static void main(String[] args) {
        int[] arr = {1, 1, 2, 0, 9, 3, 12, 7, 8, 3, 4, 65, 22};

        CountingSort.countingSort(arr);

        for (int i : arr) {
            System.out.print(i + ",");
        }
    }

    private static void countingSort(int[] arr) {
        int maxValue = getMaxValue(arr);
        countingSort(arr, maxValue);
    }

    private static int[] countingSort(int[] arr, int maxValue) {
        int bucketLen = maxValue + 1;
        int[] bucket = new int[bucketLen];

        for (int value : arr) {
            bucket[value]++;
        }

        int sortedIndex = 0;
        for (int j = 0; j < bucketLen; j++) {
            while (bucket[j] > 0) {
                arr[sortedIndex++] = j;
                bucket[j]--;
            }
        }
        return arr;
    }

    private static int getMaxValue(int[] arr) {
        int maxValue = arr[0];
        for (int value : arr) {
            if (maxValue < value) {
                maxValue = value;
            }
        }
        return maxValue;
    }
}

桶排序

桶排序

基本原理：

  1. 在额外空间充足的情况下，尽量增大桶的数量
  2. 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83

import java.util.Arrays;

/**
 * @className: BucketSort
 * @description: 桶排序
 * @author: hahaen
 **/
public class BucketSort {
    public static void main(String[] args) {
        int[] arr = {1, 1, 2, 0, 9, 3, 12, 7, 8, 3, 4, 65, 22};

        BucketSort.bucketSort(arr, 5);

        for (int i : arr) {
            System.out.print(i + ",");
        }
    }

    private static void bucketSort(int[] arr, int bucketSize) {

        int minValue = arr[0];
        int maxValue = arr[0];
        for (int value : arr) {
            if (value < minValue) {
                minValue = value;
            } else if (value > maxValue) {
                maxValue = value;
            }
        }

        int bucketCount = (int) Math.floor((maxValue - minValue) / bucketSize) + 1;
        int[][] buckets = new int[bucketCount][0];

        // 利用映射函数将数据分配到各个桶中
        for (int i = 0; i < arr.length; i++) {
            int index = (int) Math.floor((arr[i] - minValue) / bucketSize);
            buckets[index] = arrAppend(buckets[index], arr[i]);
        }

        int arrIndex = 0;
        for (int[] bucket : buckets) {
            if (bucket.length <= 0) {
                continue;
            }
            // 对每个桶进行排序，这里使用了插入排序
            insertSort(bucket);
            for (int value : bucket) {
                arr[arrIndex++] = value;
            }
        }
    }

    private static int[] arrAppend(int[] arr, int value) {
        arr = Arrays.copyOf(arr, arr.length + 1);
        arr[arr.length - 1] = value;
        return arr;
    }

    /**
     * 插入排序
     *
     * @param arr
     * @return
     */
    private static int[] insertSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            // 记录要插入的数据
            int tmp = arr[i];
            // 从已经排序的序列最右边的开始比较，找到比其小的数
            int j = i;
            while (j > 0 && tmp < arr[j - 1]) {
                arr[j] = arr[j - 1];
                j--;
            }
            // 存在比其小的数，插入
            if (j != i) {
                arr[j] = tmp;
            }
        }
        return arr;
    }

}

基数排序

基数排序

基本原理：

  1. 基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。
  2. 由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92

import java.util.Arrays;

/**
 * @className: RadixSort
 * @description: 基数排序
 * @author: hahaen
 **/
public class RadixSort {
    public static void main(String[] args) {
        int[] arr = {1, 1, 2, 0, 9, 3, 12, 7, 8, 3, 4, 65, 22};

        RadixSort.radixSort(arr);

        for (int i : arr) {
            System.out.print(i + ",");
        }
    }

    private static void radixSort(int[] arr) {
        int maxDigit = getMaxDigit(arr);
        radixSort(arr, maxDigit);
    }

    /**
     * 获取最高位数
     *
     * @param arr
     * @return
     */
    private static int getMaxDigit(int[] arr) {
        int maxValue = getMaxValue(arr);
        return getNumLenght(maxValue);
    }

    private static int getMaxValue(int[] arr) {
        int maxValue = arr[0];
        for (int value : arr) {
            if (maxValue < value) {
                maxValue = value;
            }
        }
        return maxValue;
    }

    protected static int getNumLenght(long num) {
        if (num == 0) {
            return 1;
        }
        int lenght = 0;
        for (long temp = num; temp != 0; temp /= 10) {
            lenght++;
        }
        return lenght;
    }

    private static int[] radixSort(int[] arr, int maxDigit) {
        int mod = 10;
        int dev = 1;

        for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
            // 考虑负数的情况，这里扩展一倍队列数，其中 [0-9]对应负数，[10-19]对应正数 (bucket + 10)
            int[][] counter = new int[mod * 2][0];

            for (int j = 0; j < arr.length; j++) {
                int bucket = ((arr[j] % mod) / dev) + mod;
                counter[bucket] = arrayAppend(counter[bucket], arr[j]);
            }

            int pos = 0;
            for (int[] bucket : counter) {
                for (int value : bucket) {
                    arr[pos++] = value;
                }
            }
        }

        return arr;
    }

    /**
     * 自动扩容，并保存数据
     *
     * @param arr
     * @param value
     * @return
     */
    private static int[] arrayAppend(int[] arr, int value) {
        arr = Arrays.copyOf(arr, arr.length + 1);
        arr[arr.length - 1] = value;
        return arr;
    }
}

讲讲广度优先遍历和深度优先遍历？

  • 广度优先遍历：从上往下对每一层依次访问，在每一层中，从左往右访问结点，访问完一层就进入下一层，直到没有结点可以访问为止。
  • 深度优先遍历：对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。
更新于 2022-03-11
返回 | 主页